Però els escacs també ens sorprenen quan enfoquem els números a nivell qualitatiu.
Si observem la forma dels moviments que tracen les peces, ens trobem que els escacs es regeixen per una geometria pròpia que desafia la racional geometria euclidiana. Ho podem veure molt clar en el moviment del rei (la peça que es mou de forma més simple).
 |
En canvi, en els escacs, el rei necessita el mateix nombre de moviments per recórrer un costat (un catet) que per recórrer la diagonal completa (la hipotenusa). Així doncs, la diagonal no mesura onze escacs sinó que mesura vuit escacs, els mateixos que un costat del tauler. Això dóna lloc a situacions i combinacions que desafien la lògica geomètrica a la qual estem acostumats.
Sempre hem sentit a dir que, en un pla, el camí més curt entre dos punts és una línia recta. En el pla dels escacs, hi ha molts "camins més curts" diferents de la recta.
Vegem. El trajecte més curt perquè el rei vagi des de 'e1' fins a 'e8', és de set jugades anant en línia recta. Fins aquí entra en lo racional. El sorprenent és que hi ha 393 maneres d'anar des de 'e1' a 'e8' en set jugades, és a dir, 393 camins més curts per recórrer la mateixa distància!
 |
| A l'esquerra, veiem com exemple dos possibles camins per anar de 'e1' a 'e7' en set jugades. A la dreta, es mostra el mapa complet de recorreguts segons el càlcul de Karl Fabel, matemàtic i compositor de problemes d'escacs. Els números indiquen els moviments possibles per arribar a cada casella des 'e1' amb el mínim de moviments. Per exemple, per anar a 'd2' amb una jugada, només s'hi pot arribar d'una manera. A 'e3' s'hi pot arribar de tres maneres en dues jugades: passant per 'd2', per 'e2' o per bé per 'f2'. A 'c6', s'hi pot arribar de trenta maneres diferents en cinc moviments. A 'e8', hi podem arribar amb 393 recorreguts diferents, tots ells en set moviments. |
Vegem ara una combinació d'escacs real, un famós final de reis i peons compost per Richard Réti, on es posa clarament de manifest aquest particular concepte geomètric.
En la posició de Réti, les blanques juguen i aconsegueixen unes taules contra tot pronòstic.
 |
| A l'esquerra, posició inicial de l'estudi de Réti. (Juguen blanques i igualen). A la dreta, Richard Réti |
A primer cop d'ull, sembla el jugador de les blanques hauria d'abandonar. Si el rei blanc intenta perseguir el peó negre mai el podrà atrapar i el peó acabarà convertint-se en dama. (1.Rh7 h4 2.Rh6 h3 2.Rh5 h2 2.Rh4 h1=D+). Per altra banda, si les blanques opten per avançar el seu peó, el rei negre el captura ràpidament (1.c7 Rb7 2.c8=D+ RxD).
Sembla impossible, però gràcies a la peculiar geometria dels escacs, el rei blanc pot acostar-se als dos peons al mateix temps i controlar els dos extrems del tauler. Vegem la combinació:
Seguim amb els camins del rei. Podríem preguntar-nos: De quantes maneres un rei pot passar per tots els escacs del tauler sense passar dues vegades per una mateixa casella? Hi ha moltíssims camins possibles, però com a curiositat, vegem un recorregut ideat per I. Ghersi, en el qual els nombres de cada casella que defineixen l'ordre del recorregut formen un quadrat màgic. Els vuit números col·locats en les caselles de totes les files, de totes les columnes i de les dues diagonals majors, donen sempre la mateixa suma: 260. Un bell camí.
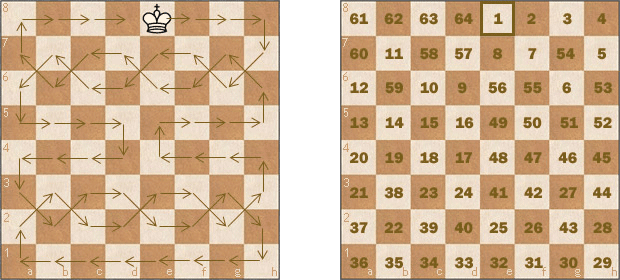 |
| Un camí del rei que forma un quadrat màgic |
No només els camins del rei son "misteriosos i inescrutables". Cada peça té les seves característiques i els seus propis camins. Posem per exemple un cavall sobre un tauler buit. En cada moviment que realitza, la casella de destí canvia de color, així que, un cavall pot arribar a qualsevol casella (a diferència dels alfils que només poden arribar a la meitat de les caselles del tauler, les del seu color).
Un clàssic i conegut problema es el de les rutes del cavall que passen per tots els escacs del tauler sense passar més d'una vegada per cada casella.
El primer llibre conservat sobre estratègia dels escacs, el Kitab Ash-Shatranj (llibre del Shatranj) escrit per Al-Suli a principis del segle X, ja contenia la primera descripció coneguda del problema de la ruta del cavall.
 |
| Una de les molts milions de milions de possibles rutes obertes del cavall. |
En canvi, si que s'ha pogut calcular el nombre possible de rutes del cavall en les quals la casella final és la mateixa que la inicial, anomenades rutes tancades, i aquí tornen a aprarèixer grans nombres:
S'ha calculat que en un tauler de 8 × 8, hi ha exactament 26.534.728.821.064 possibles rutes tancades de cavall.
(Per aprofundir més sobre números i escacs, vegeu el llibre Ajedrez y Matemáticas, d'E. Bonsdorff, K. Fabel i O. Riihimaa).
No és d'estranyar dons, que, al llarg de la història, grans matemàtics hagin experimentat en el fèrtil terreny dels escacs. Per citar-ne alguns: Leonhard Euler, Carl Friedrich Gauss, Abraham De Moivre, Adrien Marie Legendre, Henry Dudeney, Lewis Carroll... (Vegeu-ne aquí una llista molt completa).
 |
| Matemàtics escaquistes: Euler, Gauss, De Moivre, Legendre, Dudeney i Carroll |
I a l'inrevés, reconeguts escaquistes d'èlit van ser també destacats matemàtics: Adolf Anderssen, Wilhelm Steinitz, Emanuel Lasker, Max Euwe, Mikhail Botvinnik, i més recentment, John Nunn.
 |
| Escaquistes matemàtics: Anderssen, Steinitz, Lasker, Euwe, Botvinnik i Nunn |
Infinit, no. Etern, tampoc. Però comparant-ho amb la nostra escala, amb el nostre univers i amb la nostra intel·ligència i imaginació, podem afirmar que els escacs són inesgotables. Sempre es podrà descobrir alguna cosa nova, sempre es podrà evolucionar el joc amb nous conceptes, sempre ens seguiran sorprenent petits detalls de la seva enorme bellesa amagada que mai acabarem de conèixer del tot.

Cap comentari:
Deixa la teva opinió o comentari